Uniform-Price Call Auctions: A Better Way to Trade Tokens?
Analysis of call auctions for DEXs and an algorithm in Motoko
Summary
We analyze uniform-price call auctions relative to the common central limit order book exchanges, study the clearing mechanism and provide:
an online playground
a Mops package
The clearing algorithm has linear complexity in the number of orders that are executed in the trade.
Continuous trading
Continuous trading means that when a market participant places an order on an exchange then it gets executed immediately if it can. The two most common examples are central limit order books (CLOB) and automated market makers (AMM). In a CLOB the new order either matches an existing limit order, in which case it is executed immediately, or does not match an existing limit order, in which case it is placed in the order book and can be matched immediately against the next order that is coming in from another market participant. In an AMM the order is executed immediately against the liquidity pool.
An alternative are call auctions. In this type of market, orders are only “called” during a set period and executed all at once at the end of the period. Moreover, call auctions often deploy a clearing mechanism that determines one price and then execute all orders (whose limit allows) at this price. Such auctions are called uniform-price or single-price call auctions. The price is chosen to maximise exchange volume.
Central limit order books (CLOB)
Continuous trading implies that the timing of the order relative to other market participants’ actions are crucial. Markets based on CLOBs can suffer from the following problems:
Information leakage. Large orders sitting and waiting in an open order book reveal information about the intentions of market participants.
Slippage. Large orders, if executed as a “taker”, will experience slippage.
Dispersed liquidity. To reduce information leakage, market participants tend to spread out large orders into multiple smaller ones over time. This reduces the liquidity that is available to the exchange at any point in time.
Volatility. Dispersed liquidity increases volatility and the risk of short-duration price spikes.
Front-running. Sensitivity to timing enables front-running by other market participants.
Market manipulation. The open order book can be used to influence the price expectation of other market participants. Short-term price spikes can be used to trigger liquidations in futures markets.
Intransparency. CLOBs are mostly implemented as private exchanges (CEX). Since their inner workings are not transparent and since order timing is crucial this can present a problem. For example, it is difficult to assure users that they are not being frontrun by the exchange itself.
Automated market makers (AMM)
AMMs1 remove some of the above mentioned problems. Information leakage, for the lack of a public order book, is generally not an issue. Liquidity is concentrated in the form of a liquidity pool. As a result, short-duration price spike and related market manipulation may be reduced, though the extend to which this is the case depends on the depth of the liquidity pool, not the other market participants. AMMs are mostly implemented as smart contracts and therefore transparent.
However, slippage can be larger and as a result make the exchange more costly to users. This is because slippage is inherently designed into an AMM as the features that pays the liquidity pool for the risk that it takes. Moreover, since orders are executed immediately, an AMM is still sensitive to front-running. In fact, front-running has proven to be the largest problem for AMMs on chains with MEV.
Uniform-price call auctions
Uniform-price call auctions are well-known and used in traditional finance. Stock exchanges employ them for opening and closing prices and they're used in bond markets, electricity trading, and carbon emission allowance sales. Here's how they work:
Orders are collected over a set period but remain hidden from the public.
When the period ends a single clearing price is determined.
All trades execute at this price, regardless of original bids or asks.
A summary is published including at least the clearing price and the total volume exchanged.
Moreover, partial information can be published during the collection period such as an indicative clearing price and an indicative trade volume.
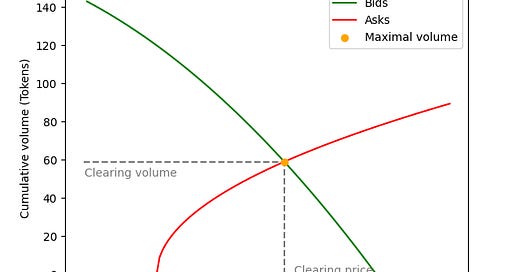
How the clearing price is determined can be seen in the following type of diagram which is known as the depth chart in CLOB exchanges.
The green line shows the cumulative bid volume at each given price, i.e. the volume of all bids that bid at least that price. The red line shows the cumulative ask volume at each given price, i.e. the volume of all asks that ask at most that price. In a continuous exchange the two lines never intersect. The green line touches the x-axis to the left of where the red line touches the x-axis. In our case however, since no trades execute during the collection period, the two lines do, in general, intersect. The intersection point gives the price that maximises the volume that can be traded. That price is chosen as the clearing price. If the two lines do not intersect it means that the highest bid is lower than the lowest ask, in which case there is no clearing price and no volume can be traded.
Advantages
Information leakage is removed as well as any incentive for market participants to hold back orders. There is no slippage since all orders execute at the same price. Liquidity is concentrated into the clearing events, not dispersed over time. This reduces volatility, short-time price spikes and the susceptibility to market manipulation. Since all orders execute at the same time there can be no front-running.
Moreover, the facts that orders are hidden and that there is no slippage encourage more aggressive bidding, closer to the real limits of the participants. This generally leads to more accurate and fairer price discovery.
Publishing the indicative clearing price and volume during the collection period may further incentivise bidding and reduce volatility.
Uniform-price call auctions are more compute intensive than AMMs but less then CLOBs, which make them a good candidate for an on-chain exchanges. The amount of data required to store the entire historical trade activity is significantly less than with a CLOB.
For a user, it is significantly easier to record, document and archive the user’s own trading activity. Placing a single order on a CLOB can result in hundreds of small trades, all at different prices. In a uniform-price call auction a single order results in a single trade at a single price or no trade at all.
Details
In this section, we'll explain the clearing mechanism in detail and show how to code it in Motoko. At the core is an algorithm that takes all the bids and asks and finds the price for which the volume that can be traded at this price is maximal.
Example 1
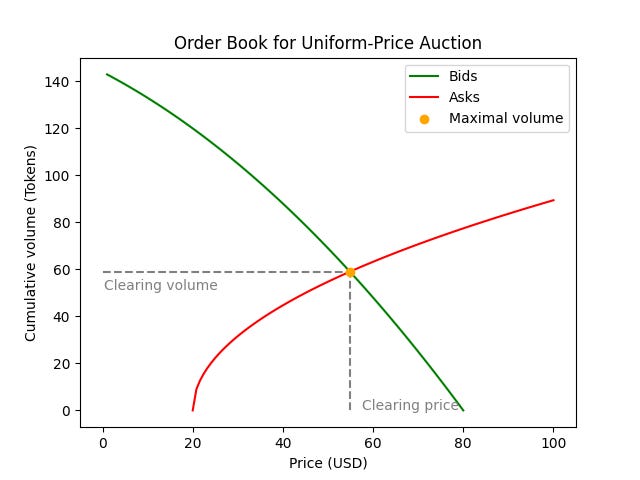
Say there are three bids for 10 tokens each with limits of $10, $20 and $30, respectively, and three asks for 10 tokens each with limits of $10, $20 and $30, respectively. Note that only a single price is allowed at which all orders have to execute. This means we cannot simply match the $10 bid with the $10 ask, the $20 bid with $20 ask, and the $30 bid with the $30 ask as that would lead to 3 different prices. Instead, we have to ask for each price p what volume would be traded at p? And then find the p for which this volume reaches a maximum. At p = $10 all bids can trade but only the lowest ask. The tradable volume is therefore 10 tokens (the one offered by the lowest ask). At p = $20 two bids and two asks can trade, making the tradable volume 20 tokens. At p = $30 only the highest bid can trade, but all asks can, making the trading volume 10 tokens. The maximum volume is reached at p = $20. Hence the clearing price is $20 and the trade volume is 20 tokens.
The following diagram illustrates the example. The green area shows cumulated bids, the red area shows cumulated asks, and the yellow area shows the trade volume possible at each price.

Auction playground
Examples like this can be explored and changed in real time in our auction playground. For all examples above and below we provide live links under the screenshots which have the orders pre-configured that were used in that example.
Mathematical definition
Mathematically, this is defined as follows. We have a trading pair between two currencies, the quote currency (often USD) and the base currency (usually a crypto token). Orders are divided in bids and asks and each order has a price denominated in quote currency per unit of base currency and a volume denominated in base currency. The price is understood as a limit. The algorithm seeks to maximise the trade volume when measured in base token.
For each price p we define the sets
and
For a set S of orders (bids or asks), we write volume(S) for the sum of the volumes of all orders in S. Then
is the cumulative volume of all bid orders that can execute at price p. Analogously,
is the cumulative volume of all ask orders that can execute at price p. The trade volume at price p is then
We have to find the price p for which t_p reaches its maximum. That price p is the clearing price and the trade volume is t_p.
In general, there is not a single price p for which t_p reaches its maximum but a range as shown in the next example. There are multiple options to set the clearing price by taking
the lower end of the range
the higher end of the range
the midpoint of the range
We choose the first option in our implementation. In other words, the clearing price is the lowest price that maximises the trade volume.
Example 2
Assume we have three bids with volume 10 tokens and limit $10, $20, $30, respectively, as above. Assume we have three asks with volume 10 tokens and limit $5, $15, $25, respectively. Then the maximum value for t_p is 20 tokens and it is reached for the price range $15 <= p <= $20. Therefore, the clearing price is $15 and the trade volume is 20 tokens.

Breaking ties
In general, at the clearing price p, the values a_p and b_p are not equal. For example, if we have a_p < b_p this means that all asks in Asks_{<= p} can be filled but not all bids in Bids_{>= p}. The bids with the highest limit should be filled first, leaving the bids with the lowest limit last.
If there is exactly one lowest bid in Bids_{>= p} then it will get partially filled. If there are multiple lowest bids then we speak of a “tie”. We have to decide which one takes precedence in getting filled.
There are multiple options to break the tie:
the orders are timestamped and the oldest one gets precedence
the orders are timestamped and the youngest one gets precedence
all are filled on a pro-rate basis
We choose the first option for our implementation.
Example 3
Say in Example 2 everything is unchanged except that the volume of the bid at $30 is 15 tokens. Since the $30 bid takes precedence over the $20 bid, the $30 will be filled completely with 15 tokens and the $20 will be partially filled with 5 tokens. The clearing price total trade volume are unchanged.

Example 4
If the volume of the $30 bid increases further to 20 tokens then it will be completely filled and the $20 bid will be unfilled. Note that the price range that maximises t_p has changed to $15 - $30 but that does not change the clearing price.

Example 5
If the volume of the $30 bid is 25 tokens then the maximum trade volume will be 25 tokens at the range $25 - $30 so the clearing price will change to $25. Now the highest ask at $25 will be partially filled with 5 tokens.
Algorithm 1
We now present an algorithm in Motoko that returns the price range of maximal volume. The caller can then decide which price point inside the range is the clearing price.
It is assumed that we have bids and asks given in two sorted Arrays where bids are sorted in from high to low and asks are sorted from low to high.
type Order = {
price : Nat;
quantity : Nat;
};
let bids : [Order] = [
{ price = 30; quantity = 150},
{ price = 20; quantity = 100},
{ price = 10; quantity = 100},
];
let asks : [Order] = [
{ price = 5; quantity = 100},
{ price = 15; quantity = 100},
{ price = 25; quantity = 100},
];
The algorithm walks simultaneously through both Arrays and, while doing that, accumulates the order volumes on each side. The next step in the walk is always taken on the side that has the lower accumulated volume. However, if both sides have equal accumulated volume then the algorithm takes a step on both sides at once. It does so until the prices cross over, i.e. until the bid becomes smaller than the ask.
class Index() {
public var index = 0;
public var isNew = true;
public func advanceIf(b : Bool) {
if (b) index += 1;
isNew := b;
};
};
func clearAuction(bids : [Order], asks : [Order]) : {
range : (Nat, Nat);
volume : Nat
} {
var range = (0, 0);
var bidVolume = 0; // cumulative volume
var askVolume = 0; // cumulative volume
var bidSide = Index();
var askSide = Index();
label L while (bidSide.index < bids.size() and askSide.index < asks.size()) {
let bid = bids[bidSide.index];
let ask = asks[askSide.index];
if (bid.price < ask.price) break L;
range := (ask.price, bid.price);
if (bidSide.isNew) bidVolume += bid.quantity;
if (askSide.isNew) askVolume += ask.quantity;
// advance indices for the next iteration
bidSide.advanceIf(bidVolume <= askVolume);
askSide.advanceIf(askVolume <= bidVolume);
};
{
range = range;
volume = Nat.min(bidVolume, askVolume);
};
};Notes:
The input arrays have to be sorted by order price. There can be multiple orders at the same price. The bids array has to be sorted in ascending price order and the asks array in descending price order.
If no orders can be cleared then a clearing volume of 0 is returned. In this case, the clearing price is meaningless and is set to 0. For example, this happens if one of the input arrays is empty or if the lowest ask is higher than the highest bid.
You can run the Motoko code live with your own input in the live link.
Algorithm 2
We now present a second implementation which has two nested loops instead of a single loop. It steps the bids in an outer loop and asks in an inner loop. Since such an approach cannot step both sides at once, it has to track additional information to handle the case when the accumulated volumes on both sides are equal.
If we are only interested in knowing the lower end of the range as the clearing price, not the full range, then the additional tracking isn’t necessary. We show this simpler algorithm first:
func clearAuction(bids : [Order], asks : [Order]) : {
price : Nat;
volume : Nat
} {
var bidVolume = 0; // cumulative volume
var askVolume = 0; // cumulative volume
var price = 0;
var i_bid = 0;
var i_ask = 0;
// invariant here: askVolume >= bidVolume
label L while (i_bid < bids.size()) {
let bid = bids[i_bid];
if (bid.price < price) break L;
bidVolume += bid.quantity;
while (askVolume < bidVolume and i_ask < asks.size()) {
let ask = asks[i_ask];
if (ask.price > bid.price) break L;
price := ask.price;
askVolume += ask.quantity;
i_ask += 1;
};
i_bid += 1;
};
{ price; volume = Nat.min(bidVolume, askVolume) };
};Now we add the additional tracking into it to be able to return the full range of maximum volume:
func clearAuctionRange(bids : [Order], asks : [Order]) : {
range : (Nat, Nat);
volume : Nat
} {
var bidVolume = 0;
var askVolume = 0
var ask_price = 0;
var bid_price = 0;
var i_bid = 0;
var i_ask = 0;
label L while (i_bid < bids.size()) {
let bid = bids[i_bid];
if (bid.price < ask_price) break L;
let wasEqual = bidVolume == askVolume;
if (not wasEqual) bid_price := bid.price;
bidVolume += bid.quantity;
while (askVolume < bidVolume and i_ask < asks.size()) {
let ask = asks[i_ask];
if (ask.price > bid.price) break L;
if (wasEqual) bid_price := bid.price;
ask_price := ask.price;
askVolume += ask.quantity;
i_ask += 1;
};
i_bid += 1;
};
{
range = (ask_price, bid_price);
volume = Nat.min(bidVolume, askVolume);
};
};Mops package
Extended version of the last two algorithms are published on mops: https://mops.one/auction
The extensions include:
input accepted as Iterators instead of Arrays
generic price type (type parameter) so that the price type can be Nat, Int or Float
robust against edge cases such as orders with volume 0
We look forward to a fully on-chain, decentralized and fair exchange based on uniform-price call auctions.